Basics

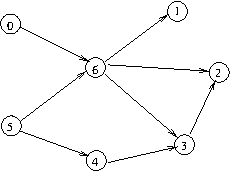
A directed acyclic graph (DAG) is a directed graph having no cycle.

Directed acyclic graphs are often used for representing dependency relations, for example:

• vertices are activities in a project, and an edge (x,y) means that activity y cannot start before activity x is completed (because y depends on the end product of x);
• vertices are topics in a book, and an edge (x,y) means that topic y cannot be understood without first understanding topic x;
• vertices are computation steps or computation results, and an edge (x,y) means that computing y takes as inputs the result for x.

DAG example

Cycle-containing graph

Topological sorting

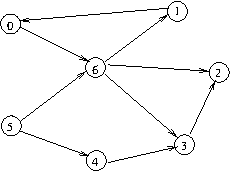
Often, when dependency relations are involved, the following two problems need to be solved:

1. Find if there is any circular dependency (in other words, if the dependency graph is a DAG or not);
2. Put the items in an order compatible with the dependency restrictions, that is, put the vertices in a list such that whenever there is an edge (x,y), then x comes before y in that list.

The latter problem is called topological sorting. Note that the solution is not, generally, unique.

Finding if a directed graph has cycles or not is done while attempting to do the topological sorting.

Property: Topological sorting is possible, for a directed graph, if and only if there are no cycles in the graph.

If a graph has a cycle, then it is obvious that topologically sorting it is impossible: Suppose we have a topological sorting, and let x be the first vertex from the cycle that appears in the topological sorting. Then, let y be the preceeding vertex in that cycle; we have the edge (y,x), but y comes after x in the topological sorting, which is not allowed.

For proving the other way round, we use the construction algorithms below. We'll prove that neither one fails unless there is a cycle in the input graph.

Predecessor counting algorithm