file:///Users/raluca/Downloads/lab4.pdf

Theory

DAG (Directed acyclic graph)

• a directed graph having no cycle
• often used for representing dependency relations, for example:
  • vertices are activities in a project, and an edge (x,y) means that activity y cannot start before activity x is completed (because y depends on the end product of x)
  • vertices are topics in a book, and an edge (x,y) means that topic y cannot be understood without first understanding topic x
  • vertices are computation steps or computation results, and an edge (x,y) means that computing y takes as inputs the result for x
• Property: A directed graph is a DAG if and only if it has no loops and each of its strongly connected components consists in a single vertex.

Examples

DAG:

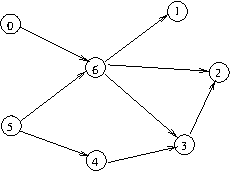
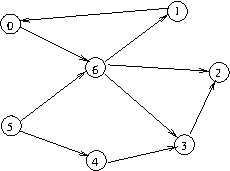
Cycle-containing graph:

Topological sorting

Often, when dependency relations are involved, the following two problems need to be solved:

1. Find if there is any circular dependency (in other words, if the dependency graph is a DAG or not)
2. Put the items in an order compatible with the dependency restrictions, that is, put the vertices in a list such that whenever there is an edge (x,y), then x comes before y in that list

• Property: topological sorting is possible, for a directed graph, if and only if there are no cycles in the graph
• If a graph has a cycle, then it is obvious that topologically sorting it is impossible: Suppose we have a topological sorting, and let x be the first vertex from the cycle that appears in the topological sorting. Then, let y be the preceeding vertex in that cycle; we have the edge (y,x), but y comes after x in the topological sorting, which is not allowed.

For proving the other way round, we use the construction algorithms below. We'll prove that neither one fails unless there is a cycle in the input graph.

Predecessor counting algorithm